Elettromagnetismo

1 Fondamenti

1.1 Campo elettromagnetico PSW

Il campo elettromagnetico è un campo di forze. Le leggi che regolano il campo elettromagnetico sono:

legge di Faraday
legge di Ampere
legge di Gauss
legge di Gauss magnetica
legge di conservazione della carica.

Le prime quattro leggi costituiscono le leggi di Maxwell, le quali legano tra di loro:

il vettore intensità di campo elettrico $\underline{e}$ (in V/m)
il vettore induzione elettromagnetica $\underline{d}$ (in C/m²)
il vettore intensità di campo magnetico $\underline{h}$ (in A/m)
il vettore induzione magnetica $\underline{h}$ (in Wb/m²).

Le equazioni di Maxwell possono essere espresse in forma integrale e in forma differenziale, nel dominio del tempo e nel dominio della frequenza. Le equazioni di Maxwell indipendenti sono soltanto due:

\underline{\nabla} \times \underline{e} = - \frac{\partial \underline{b}}{\partial t}

$\underline{\nabla} \times \underline{e} = - \dfrac{\partial \underline{b}}{\partial t}$

\underline{\nabla} \times \underline{h} = \frac{\partial \underline{d}}{\partial t} + \underline{j_{i}} + \underline{j}

$\underline{\nabla} \times \underline{h} = \dfrac{\partial \underline{d}}{\partial t} + \underline{j_i} + \underline{j}$

dove $\underline{j}$ è la densità di corrente impressa dovuta a cause esterne al campo, e $\underline{j}_i$ è la densità di corrente indotta dovuta al campo.

Esse contengono 5 incognite: $\underline{e}$ , $\underline{h}$ , $\underline{d}$ , $\underline{b}$ , $\underline{j}_i$ . Quindi servono 3 relazioni vettoriali per rendere determinato il problema, descrivendo il comportamento elettromagnetico del materiale in cui il campo si sviluppa; queste relazioni sono dette relazioni costitutive.

Le relazioni considerate sono macroscopiche: si considerano volumi macroscopici tali da essere abbastanza grandi da contenere una quantità importante di carica. Se considerassimo volumi troppo piccoli, sarebbe troppo evidente dove è presente e dove non è presente carica, e le leggi macroscopiche non funzionerebbero.

1.1.1 Campi trasversi

I campi elettrico e magnetico si dicono trasversi se sono entrambi ortogonali alla direzione direzione radiale/assiale (direzione di propagazione).

1.2 Propagazione PSW

1.2.1 Formula di Friis per la propagazione nel vuoto PSW

Nello spazio libero la propagazione di un segnale elettromagnetico è governata dalla formula di Friis:

P_{r} = P_{t} G_{T} G_{R} {(\frac{λ}{4 π R})}^{2}

$P_r = P_t\: G_T\: G_R\: \left( \dfrac{\lambda}{4\pi R} \right)^2$ , con:

$P_t$ , $G_T$ potenza trasmessa e guadagno dell'*antenna trasmittente;
$P_r$ , $G_R$ potenza ricevuta e guadagno dell'antenna ricevente.
$R$ distanza tra le antenne.

Quindi la potenza varia col quadrato della distanza.

1.2.2 Propagazione in ambiente urbano PSW

Se siamo nel vuoto, le condizioni di propagazione differiscono in maniera importante, ad esempio per effetto del suolo o dei palazzi. In ambito urbano si deve tener conto nella valutazione della potenza ricevuta di tre termini principali: fading rapido, fading lento, e un terzo contributo dominante che varia in funzione della distanza $R$ .

1.2.3 Volume di rispetto PSW

Il volume di rispetto è un volume tale per cui il campo elettromagnetico non deve superare, all'esterno di esso, il valore massimo di potenza stabilito per legge.

Piano laterale e piano verticale
Per studiare la propagazione in ambiente urbano, si considera la propagazione relativamente a due piani geometrici:
- piano laterale la propagazione avviene per riflessioni multiple fra ostacoli. Il segnale viaggia attorno o attraversa tali ostacoli. È un'attenuazione molto forte, e si hanno diversi cammini multipli. Nel caso di microcelle ci si limita a studiare il piano laterale.
- Piano verticale piano contenente le due antenne. L'attenuazione è meno accentuata rispetto a quella del piano laterale. All'aumentare della distanza, i cammini tra le due antenne si fanno sempre più intricati. Nel caso delle macrocelle ci si limita a studiare il piano verticale.

1.2.4 Come si studia la propagazione in ambiente umano PSW

Per studiare la propagazione del segnale elettromagnetico in ambiente urbano, bisognerebbe tener conto di tutti gli edifici e di tutte le loro caratteristiche (geometria, materiali utilizzati, ecc.). Siccome una tale stima è molto difficile, si preferisce per praticità mediante stima aleatoria dell'ambiente (o modello probabilistico, o modello di previsione della propagazione) o mediante campagne di misura sul luogo.

Nei servizi di telecomunicazione moderni come la telefonia mobile, bisogna tener conto di:

l'alterazione massima del segnale;
le interferenze tra celle differenti funzionanti alla stessa frequenza.

1.2.5 Caratteristiche della propagazione per ambienti urbani PSW

Si considerano due antenne trasmittente Tx e ricevente Rx, poste a distanza $R$ tale da considerarle in campo lontano (cioé in zona di Fraunhofer): la distanza $R$ è cioè molto più grande rispetto alle dimensioni delle sorgenti del campo. La formula di Friis afferma che la potenza $P_R$ ricevuta da un'antenna Rx è, in condizioni di spazio libero:

P_{R} = \frac{G_{T} G_{R} λ^{2}}{(4 π)^{2} R^{2}} P_{T} = \frac{P_{T} A}{R^{2}}

$P_R = {\frac{G_TG_R\lambda^2}{{(4\pi)^2R^2}}P_T} = \frac{P_TA}{R^2}$

con:

$G_T$ e $G_R$ guadagni rispettivamente delle antenne Tx ed Rx
$\lambda$ lunghezza d'onda del segnale portante radio
$A$ parametro costante, una volta fissate le antenne e la frequenza del collegamento
$P_T$ potenza emessa dall'antenna trasmittente.

La variazione con la distanza del tipo $1/R^2$ non consente il riutilizzo delle frequenze, in quanto il segnale non sarebbe sufficientemente attuenato tra zone differenti di una stessa area metropolitana. È possibile utilizzare l'approssimazione di terra piatta, nel caso di antenne in vicinanza del suolo e di stazioni radiobase in posizioni non troppo elevate. Allora la potenza ricevuta $P_R$ vale:

P_{R} = \frac{P_{T} A}{R^{4}}

$P_R = \frac{P_TA}{R^4}$

Per la propagazione in ambiente urbano, nel caso di spazio libero e stazioni radiobase poste in punti elevati, l'andamento della potenza ricevuta con la distanza è del tipo $1/R^n$ , con $n$ (detto index range) tipicamente tra 3 e 4 Se le stazioni radiobase sono poste in punti non particolarmente elevati, $n$ può essere maggiore di 4. Inoltre si hanno variazioni aleatorie significative, dovute al fast fading e allo shadow fading. All'interno degli edifici, la propagazione del segnale presenta caratteristiche differenti. Per la copertura di una singola area metropolitana, si suddivide l'area in un numero $N$ di regioni in cui si riutilizza lo stesso insieme di $N_c$ canali in frequenza. Il numero totale di chiamate simultanee è $NN_c$ . Ognuna delle $N$ regioni è suddivisa in $N_R$ celle, ciascuna operante a una certa frequenza assegnata da una stazione radiobase. Si utilizza lo stesso canale in frequenza per celle la cui distanza è abbastanza grande da mantenere l'interferenza accettabile.

Copertura di una zona con celle lineari (es. autostrada)

Si vuole realizzare la copertura di una zona lineare (figura). Considerando il problema come monodimensionale, si suddivide ciascuna delle due regioni in $N_R$ celle di raggio $r_c$ . La cella $1$ opera a frequenza $f_1$ , la cella $2$ a frequenza $f_2$ , la cella $3$ a frequenza $f_3$ , ecc. Quando un utente si trova nella frontiera tra le celle $1$ e $2$ della regione $1$ , allora riceverà in downlink la minima potenza $P$ (essendo alla massima distanza $r_c$ dalla stazione radiobase (RBS) della cella $1$ ) e la massima interferenza $I$ dalla cella $1$ della regione $2$ (in quanto le celle $1$ delle due regioni utilizzano la stessa frequenza di trasmissione). Se ad esempio $N_R = 3$ , la distanza dell'utente dalla RBS della cella $1$ della regione $2$ è pari a $5r_c$ . Per un numero $N_R$ generico si ha che la distanza fra la più vicina stazione radiobase interferente e il terminale mobile è $(2N_R - 1)r_c$ . La potenza $S$ del segnale che arriva al terminale mobile vale:

$S = \frac{P_{T} A}{r_{c}^{n}} .$ $S = \frac{P_TA}{r_c^n}.$

Il segnale interferente vale invece:

$I = \frac{P_{T} A}{[(2 N_{R} - 1) r_{c}]^{n}}$ $I = \frac{P_TA}{[(2N_R -1 )r_c]^n}$

essendo $n$ l'indice di attenuazione (2 nello spazio libero, tra 2 e 4 in ambiente urbano), $P_T$ la potenza di trasmissione delle stazioni radiobase, che si suppone uguale per tutte e 6. Il rapporto tra potenza di segnale e potenza di interferenza nel caso peggiore di bordo cella è:

$\frac{S}{I} = \frac{\bcancel P_{T} \bcancel A}{\bcancel r_{c}^{n}} \frac{[2 N_{R} - 1]^{n} \cancel r_{c}^{2}}{\cancel P_{T} \cancel A} = (2 N_{R} - 1)^{n} .$ $\frac{S}{I} = \frac{\bcancel{P_T}\bcancel{A}}{\bcancel{r_c^n}}\frac{[2N_R - 1]^n\cancel{r_c^2}}{\cancel{P_T}\cancel{A}} = (2N_R - 1)^n.$

Tipicamente il valore di $S/I$ richiesto dev'essere superiore a $17\ dB$ . Nel caso di spazio libero ( $n=2$ ) per avere un rapporto $S/I$ superiore a $17\ dB$ devo avere minimo $N_R = 4$ celle per regione: $20Log[2(4)-1]^2 = 33.8\ dB$ . Per attenuazioni più forti (es. $n=4$ ), $N_R$ può anche essere uguale a 2. L'obiettivo è quello di utilizzare il minor numero di stazioni radiobase, visti i costi relativi all'installazione e alla manutenzione. Nel caso di uplink il discorso è simile, ma la potenza $P_T$ trasmessa da ciascun terminale mobile può non essere la stessa.
Copertura bidimensionale di un'area metropolitana

Per il progetto della copertura bidimensionale di un'area metropolitana, si utilizzano concettualmente celle esagonali, in quanto l'esagono permette di "piastrellare" una regione piana con regolarità; inoltre l'esagono approssima i contorni circolari di uguale intensità quando la propagazione è isotropica (cioè è a uguale intensità in tutte le direzioni). Nella realtà non si hanno maglie a celle esagonali: le celle hanno una forma irregolare e sono parzialmente sovrapposte per evitare buchi nella copertura. Utilizzando celle esagonali, il riuso del canale prevede di suddividere la zona in regioni composte ciascuna da 7 celle (figura). Un insieme di celle adiacenti che utilizzano tutte le frequenze (canali) disponibili è detto cluster. Le celle a frequenze diverse si dicono disgiunte, quelle che utilizzano la stessa frequenza si dicono di co-canale. Se i trasmettitori sono posti a centro cella, le celle di co-canale giacciono su un perimetro circolare detto tier attorno alla cella centrale. Con le celle esagonali e regioni di 7 esagoni, si hanno 6 celle di co-canale poste idealmente a distanza $D$ dalla cella di riferimento. La distanza $d$ è detta distanza di riutilizzo delle frequenze. L'area di una singola cella esagonale è pari all'area dei 6 triangoli che lo compongono, ciascuno di area $A_{cella}=bh/2$ , con $b=r_c$ e $h=r_c \sin 60^{\circ}$ . Quindi l'area di una cella esagonale è $6(r_c^2/2)\sin 60^{\circ} = 3(r_c^2)sin60^{\circ}$ . Il legame tra il numero di celle $N_R$ e la distanza $D$ di riutilizzo delle frequenze è:

$A_{regione 7 celle} = N_{R} A_{cella} = D^{2} \sin 60^{\circ} = N_{R} (3 r_{c}^{2} \sin 60^{\circ}) \Rightarrow N_{R} = \frac{1}{3} (\frac{D}{r_{c}})^{2}$ $A_\text{regione 7 celle} = N_R A_\text{cella} = D^2\sin{60^\circ} = N_R(3r_c^2 \sin{60^\circ}) \Rightarrow N_R = \frac{1}{3}\Big(\frac{D}{r_c}\Big)^2$ , $\Rightarrow \frac{D}{r_{c}} = \sqrt{3 N_{R}} .$ $\Rightarrow \frac{D}{r_c} = \sqrt{3N_R}.$

Si vuole valutare l'interferenza di downlink dovuta alle celle di co-canale, supponendo che il ricevitore sia a bordo cella, sulla cella posta al centro, avente 6 celle di co-canale nei dintorni. In questa situazione due celle distano circa $D+r_c$ dalla cella dove si trova l'utente, altre due celle distano circa $D-r_c$ e le ultime due distano circa $R$ . Si assume che il segnale ricevuto dalla stazione radiobase S valga:

$S = \frac{P_{T} A}{r_{c}^{n}} .$ $S = \frac{P_TA}{r_c^n}.$

Il segnale interferente $I$ vale invece:

$I = P_{s e g n a l e i n t e r f e r e n t e} = \frac{P_{T} A}{[(2 N_{R} - 1) r_{c}]^{n}}$ $I = P_{\ segnale\ interferente} = \frac{P_TA}{[(2N_R-1)r_c]^n}$

con $P_T$ potenza di trasmissione delle base stations, che si suppone uguale per tutte e 6. L'interferenza $I$ , considerando i 6 contributi delle celle di co-canale (e trascurando i contributi di interferenza delle altre celle) vale:

$I = P_{T} A [\frac{1}{(D - r_{c})^{n}} + \frac{1}{D^{n}} + \frac{1}{(D + r_{c})^{n}} + \frac{1}{(D - r_{c})^{n}} + \frac{1}{D^{n}} + \frac{1}{(D + r_{c})^{n}}] =$ $I={P_T}{A}\bigg[\frac{1}{(D-r_c)^n}+\frac{1}{D^n}+\frac{1}{(D+r_c)^n}+\frac{1}{(D-r_c)^n}+\frac{1}{D^n}+\frac{1}{(D+r_c)^n}\bigg] =$

$= 2 \frac{P_{T} A}{R_{c}^{n}} [\frac{1}{(\frac{D}{r_{c}} - 1)^{n}} + (\frac{D}{r_{c}} + 1)^{n} + (\frac{D}{r_{c}})^{n}] =$ $= 2 \frac{P_TA}{R_c^n}\bigg[\frac{1}{(\frac{D}{r_c}-1)^n}+(\frac{D}{r_c}+1)^n+(\frac{D}{r_c})^n\bigg] =$

$= 2 \frac{P_{T} A}{r_{c}^{n}} [\frac{1}{(\sqrt{3 N_{R}} - 1)^{n}} + \frac{1}{(\sqrt{3 N_{R}} + 1)^{n}} + \frac{1}{(\sqrt{3 N_{R}})^{n}}] .$ $= 2\frac{P_TA}{r_c^n}\bigg[\frac{1}{(\sqrt{3N_R}-1)^n}+\frac{1}{(\sqrt{3N_R}+1)^n}+\frac{1}{(\sqrt{3N_R})^n} \bigg].$

Il rapporto S/I vale:

$\frac{S}{I}= \frac{\bcancel{P_T}\bcancel{A}}{\bcancel{r_c^n}} \frac{\big 1}{{\big {\frac{2 \cancel{P_T} \cancel{A}}{\cancel{r_c^n}}}}\frac{\big 1}{\bigg[ \frac{\big 1}{\big{(\sqrt{3N_R}-1)^n}}+\frac{\big 1}{(\big{\sqrt{3N_R}+1)^n}}+\frac{\big 1}{(\big{\sqrt{3N_R})^n}} \bigg]}} =$ $\frac{S}{I}= \frac{\bcancel{P_T}\bcancel{A}}{\bcancel{r_c^n}} \frac{\big 1}{{\big {\frac{2 \cancel{P_T} \cancel{A}}{\cancel{r_c^n}}}}\frac{\big 1}{\bigg[ \frac{\big 1}{\big{(\sqrt{3N_R}-1)^n}}+\frac{\big 1}{(\big{\sqrt{3N_R}+1)^n}}+\frac{\big 1}{(\big{\sqrt{3N_R})^n}} \bigg]}} =$

$= \frac{1}{2}\frac{\big 1}{\bigg[ \frac{\big 1}{\big{(\sqrt{3N_R}-1)^n}}+\frac{\big 1}{(\big{\sqrt{3N_R}+1)^n}}+\frac{\big 1}{(\big{\sqrt{3N_R})^n}} \bigg]}.$ $= \frac{1}{2}\frac{\big 1}{\bigg[ \frac{\big 1}{\big{(\sqrt{3N_R}-1)^n}}+\frac{\big 1}{(\big{\sqrt{3N_R}+1)^n}}+\frac{\big 1}{(\big{\sqrt{3N_R})^n}} \bigg]}.$

Prendendo $n=4$ (valore di $n$ tipico nella propagazione in ambiente urbano) e $N_R = 7$ , si ottiene un rapporto $S\slash I$ maggiore di $17\ dB$ . In spazio libero, con $n=2$ , il numero $N_R$ di celle necessarie per ottenere lo stesso rapporto segnale/interferenza aumenta a dismisura e risulta difficile garantire una copertura adeguata. Per aumentare il rapporto segnale/interferenza si possono usare antenne direzionali che introducono anisotropia nella copertura (il campo non varia con la direzione di irradiamento). Nelle zone in cui si ha $n > 2$ (andamento della potenza più decrescente rispetto al caso $n=2$ di spazio libero) si ha un'attenuazione più elevata che rende più difficile la copertura, ma permette al contempo di riutilizzare il canale a distanze minori.

Utilizzando $N_R=7$ celle per regione, si può dividere ciascuna cella esagonale in 3 settori e in ciascun settore si pone un'antenna di fascio $120^\circ$ . Ogni antenna è a frequenza diversa: serviranno in tal caso $7 \times 3 = 21$ bande di frequenza (una frequenza per settore), e non 7; quindi aumenta il numero di celle richieste. Con le antenne direzionali però si riduce il numero di stazioni radio-base da utilizzare, così come la distanza del terminale mobile posto a bordo cella e la stazione base interferente più vicina. L'interferenza è ridotta di un terzo (riguarda per ciascuna frequenza la regione racchiusa dall'angolo di $120^\circ$ ).

In alternativa si possono usare $N_R=21$ celle e posizionare le stazioni radio-base sul vertice della cella e non al centro. L'RBS in questo caso serve 3 celle, ognuna delle quali può essere servita con un'antenna direzionale con larghezza di fascio di $60^\circ$ . Essendo in questo caso inferiore la larghezza del fascio (rispetto al caso di cella divisa in 3 settori), si hanno meno interferenze tra stazioni radio-base alla stessa frequenza. Si può usare il modello standard di propagazione in spazio libero (quindi la formula di Friis) nel caso in cui esista un percorso diretto tra Tx ed Rx. Tuttavia in ambiente urbano esistono generalmente diversi percorsi che collegano Tx ed Rx: questi percorsi multipli permettono al segnale di arrivare a destinazione in situazioni NLOS (Non-Line Of Sight), in cui cioè le antenne Tx ed Rx non si vedono direttamente l'una con l'altra. Anche nel caso in cui le antenne Tx ed Rx siano in LOS avviene che il segnale ricevuto contenga contributi provenienti da percorsi NLOS tra Tx ed Rx.

1.2.6 Multipath e fading

Il multipath è quel fenomeno per cui al ricevitore arrivano diverse copie del segnale con diversa ampiezza e ritardo; queste copie sono chiamate echi.

Nel dominio della frequenza si distingue tra flat fading e selective fading.

Si parla di flat fading nel caso in cui la banda $B_{\text{segnale}}$ del segnale trasmesso sia molto minore della banda $B_{\text{canale}}$ del canale affetto da multipath: $B_{\text{segnale}} \ll B_{\text{canale}}$ . In tal caso tutte le componenti spettrali del segnale sono trattate dal fenomeno allo stesso modo.

Nel caso in cui $B_{\text{segnale}} > B_{\text{canale}}$ , il fading è selettivo in frequenza (selective fading). Questa differenza non tiene conto degli effetti dovuti ai movimenti reciproci tra trasmittente e ricevente.

Nel dominio del tempo, si distingue tra fading lento e fading veloce.

Il fading veloce è un fenomeno che si presenta quando il del canale è piccolo rispetto al requisito sul ritardo dell'applicazione. Ampiezza e fase del segnale variano in maniera sensibile nel tempo.

Il fading lento o shadow fading si verifica quando un ostacolo di grandi dimensioni occlude il percorso principale del segnale. Per modellare lo shadow fading si utilizza una distribuzione log-normale. Si verifica quando il del canale è elevato rispetto al requisito sul ritardo dell'applicazione.

Fading e propagazione del segnale in ambiente urbano
Il segnale che si propaga in ambiente urbano è caratterizzato da:
- 3 scale di variazione spaziale:
  - fast fading;
  - shadow fading,
  - variazione con la distanza di tipo $1/r^n$ ;
- variazioni temporali;
- polarizzazione mista.
Quando il ricevitore (Rx) si sposta lungo un ambiente urbano, il segnale dalla stazione radiobase (RBS) è ricevbuto attraverso cammini multipli. Per spostamenti dell'ordine delle decine di centimetri, il campo tende a variare considerevolmente: varia anche di 20 dB tra un punto e l'altro, cioè il campo varia con un rapporto $1:100$ . Per spostamenti dell'ordine di qualche metro, la variazione del segnale può essere anche di 30 dB (rapporto $1:1000=1:10^3$ ). Queste variaziopni rapide sono dovute alla presenza, in ambiente urbano, di riflessioni, diffrazione, scattering

1.3 Potenziali scalare elettrico e vettore magnetico PSW

Le equazioni di Maxwell scritte in termini di campo elettrico $\underline{E}(\underline{r}, t)$ e magnetico $\underline{B}(\underline{r}, t)$ , ci assicurano che esistono una funzione scalare $\phi(\underline{r}, t)$ , detta potenziale scalare elettrico, e un vettore $\underline{A}(\underline{r}, t)$ , detto potenziale vettore magnetico, tali che:

\underline{E} (\underline{r}, t) = - \frac{\partial}{\partial t} \underline{A} (\underline{r}, t) - \underline{\nabla} ϕ (\underline{r}, t)

$\underline{E}(\underline{r}, t) = -\dfrac{\partial}{\partial t} \underline{A}(\underline{r}, t) - \underline{\nabla}\phi(\underline{r}, t)$ ,

\underline{B} (\underline{r}, t) = \underline{\nabla} \times \underline{A} (\underline{r}, t)

$\underline{B}(\underline{r}, t) = \underline{\nabla} \times \underline{A}(\underline{r}, t)$ .

Le due equazioni precedenti definisco i potenziali vettore elettrico e magnetico in modo implicito e non univoco. Le seguenti equazioni, rappresentanti la cosiddetta trasformazione di gauge, lasciano inalterati i campi elettrico e magnetico:

ϕ^{'} = ϕ - \frac{\partial ψ}{\partial t} \to ϕ^{'} = ϕ - j ω ψ

$\phi'= \phi-\dfrac{\partial \psi}{\partial t} \to \phi'= \phi-j\omega \psi$ ,

\underline{A^{'}} = \underline{A} + \underline{\nabla} ψ

$\underline{A'}=\underline{A} + \underline{\nabla} \psi$ , con

ψ = ψ (r)

$\psi = \psi(r)$ funzione arbitraria.

Se si scelgono i potenzili vettore e scalare in maniera che sussista la condizione seguente (detta gauge di Lorenz):

\underline{\nabla} \cdot \underline{A} (\underline{r}, t) + \frac{1}{c^{2}} \frac{\partial V}{\partial t} = 0

$\underline{\nabla} \cdot \underline{A}(\underline{r}, t) + \dfrac{1}{c^2}\dfrac{\partial V}{\partial t} = 0$ .

Qualora i due potenziali soddisfino tale equazione, si ottengono le equazioni delle onde elettromagnetiche, ossia le equazioni di Maxwell riscritte in termini di potenziali:

\nabla^{2} \underline{A} (\underline{r}, t) - \frac{1}{c^{2}} \frac{\partial^{2} \underline{A} (\underline{r}, t)}{\partial t^{2}} = - μ_{0} J (\underline{r}, t)

$\nabla^2 \underline{A}(\underline{r}, t) - \dfrac{1}{c^2} \dfrac{\partial^2\underline{A}(\underline{r}, t)}{\partial t^2} = -\mu_0J(\underline{r}, t)$ ,

\nabla^{2} ψ (\underline{r}, t) - \frac{1}{c^{2}} \frac{\partial^{2} ψ}{\partial t^{2}} = - \frac{ρ (\underline{r}, t)}{ϵ_{0}}

$\nabla^2 \psi(\underline{r}, t) - \dfrac{1}{c^2} \dfrac{\partial^2\psi}{\partial t^2} = -\dfrac{\rho(\underline{r}, t)}{\epsilon_0}$ .

Se i campi variano lentamente, allora i potenziali risultano univocamente determinati, note le sorgenti del campo. Si possono scegliere gauge diversi da quello di Lorenz. Il potenziale scalare elettrico è definito solo a meno della derivata temporale di una funzione scalare, e il potenziale vettore magnetico a meno del gradiente della stessa funzione. Per definire i campi si introducono delle condizioni di gauge, es. fissando il valore della divergenza del potenziale vettore magnetico.

1.4 Copertura di una stazione radiobase PSW

L'area di copertura di una stazione radiobase è la zona geografica entro la quale è possibile stabilire una comunicazione bidirezionale con la qualità del servizio desideratà. La condizione necessaria è che l'attenuzione in dB $A_{\text{totale \textbf{dB}}}$ tra la stazione radiobase e il punto geografico considerato sia tale che valgano contemporaneamente le relazioni:

{\begin{cases} P_{BS \textbf{dB}} - A_{totale \textbf{dB}} + G_{MS \textbf{dB}} \geq S_{MS \textbf{dB}} \\ P_{MS \textbf{dB}} - A_{totale \textbf{dB}} + G_{BS \textbf{dB}} \geq S_{BS \textbf{dB}} \end{cases}

$\begin{cases} P_{\text{BS \textbf{dB}}} - A_{\text{totale \textbf{dB}}} + G_{\text{MS \textbf{dB}}} \geq S_{\text{MS \textbf{dB}}} \\ P_{\text{MS \textbf{dB}}} - A_{\text{totale \textbf{dB}}} + G_{\text{BS \textbf{dB}}} \geq S_{\text{BS \textbf{dB}}} \end{cases}$ ,

con:

$P_{\text{BS \textbf{dB}}}$ potenza della stazione radiobase;
$P_{\text{MS \textbf{dB}}}$ potenza del terminale mobile;
$S_{\text{BS \textbf{dB}}}$ sensibilità della stazione radiobase;
$S_{\text{MS \textbf{dB}}}$ sensibilità del terminale mobile;
$G_{\text{BS \textbf{dB}}}$ guadagno della stazione radiobase;
$G_{\text{MS \textbf{dB}}}$ guadagno terminale mobile.

L'area di copertura di un sistema radiomobile è pari all'unione di tutte le aree di copertura di tutte le stazioni radiobase.

Per stimare l'attenuazione si possono utilizzare diversi approcci

1.5 Teorema di Poynting PSW

È una relazione integrale che deve essere soddisfatta dalle soluzioni delle equazioni di Maxwell. Esprime il principio di conservazione dell'energia per il campo elettromagnetico.

1.6 Dipolo elementare PSW

Il dipolo elementare è un sistema di due fili orientati lungo un asse (es. z) con un gap nel centro. La corrente scorre anch'essa lungo l'asse z. Il campo elettrico ha due componenti $E_{r}$ ed $E_{\vartheta}$ . Il campo magnetico ha la sla componente $E_{\phi}$ . Il campo vicino ( $\beta r \ll 1$ ) è essenzialmente elettrico (la componente magnetica è trascurabile). In campo lontano ( $\beta r \gg 1$ ), i campi elettrico e magnetico non sono direttamente confrontabili.

1.6.1 Campo di un dipolo elementare

In un sistema sferico, il campo nel punto $P=(r, \vartheta, \varphi)$ prodotto da un dipolo elementare di ampiezza $I\Delta z$ posto nell'origine è:

E_{r} = j \frac{ζ I Δ z}{2 λ r} [0 + \frac{1}{j β r} + \frac{1}{(j β r)^{2}}] e^{- j β r} 2 \cos (ϑ)

$E_r = j \dfrac{\zeta I \Delta z}{2 \lambda r} \left[ 0 + \dfrac{1}{j \beta r} + \dfrac{1}{(j \beta r)^2} \right]e^{-j \beta r} 2 \cos(\vartheta)$ ,

E_{ϑ} = j \frac{ζ I Δ z}{2 λ r} [1 + \frac{1}{j β r} + \frac{1}{(j β r)^{2}}] e^{- j β r} \sin (ϑ)

$E_{\vartheta} = j \dfrac{\zeta I \Delta z}{2 \lambda r} \left[ 1 + \dfrac{1}{j \beta r} + \dfrac{1}{(j \beta r)^2} \right]e^{-j \beta r} \sin(\vartheta)$ ,

H_{φ} = j \frac{I Δ z}{2 \lamba r} [1 + \frac{1}{j β r} + 0] e^{- j β r} \sin (ϑ)

$H_{\varphi} = j \dfrac{I \Delta z}{2 \lamba r} \left[1 + \dfrac{1}{j \beta r} + 0 \right] e^{-j\beta r}\sin(\vartheta)$ .

Queste equazioni valgono ovunque nello spazio, eccetto che nel punto dove si trova il dipolo.

Punto campo lontano dal dipolo elementare

Se il punto campo è molto distante dal dipolo, cioè se $\beta r \ll 1$ , le frazioni dentro le parentesi quadre nelle espressioni del campo del dipolo elementare vanno a zero, quindi si annulla il contributo $E_r$ , e il campo diventa:

$E_{ϑ} = j \frac{ζ I Δ z}{2 λ r} e^{- j β r} \sin (ϑ)$ $E_{\vartheta} = j \dfrac{\zeta I \Delta z}{2 \lambda r} e^{-j \beta r} \sin(\vartheta)$

$H_{φ} = j \frac{I Δ z}{2 \lamba r} e^{- j β r} \sin (ϑ) = \frac{1}{ζ} E_{ϑ}$ $H_{\varphi} = j \dfrac{I \Delta z}{2 \lamba r} e^{-j\beta r}\sin(\vartheta) = \dfrac{1}{\zeta} E_{\vartheta}$ .

I campi sono quindi trasversi, e variano con $r$ allo stesso modo. Il campo si propaga in direzione radiale. Esprimendo il campo in termini vettoriali:

$\underline{E} = ζ \underline{H} \times {\underline{i}}_{r}$ $\underline{E} = \zeta \underline{H} \times \underline{i}_r$ .

Il campo lontano di un dipolo elementare è un'onda sferica con superfici sferiche equifase ed equiampiezza. In una zona limitata rispetto al raggio dell'onda sferica, la sfera risulta quasi indistinguibile dal suo piano tangente, e la possiamo approssimare a un'onda piana (sempre in una regione limitata dello spazio rispetto al raggio della sfera); quindi approssimando otteniamo un'onda piana che viaggia in direzione radiale. Per $\beta r \to \infty$ lo stesso discorso vale per il campo di più dipoli.
1. Condizioni di Sommerfeld
  
  Sono le condizioni che debbono valere affinché il campo possa essere approssimato a un'onda piana che viaggia verso l'infinito:
  
  $lim_{r \to \infty} r | \underline{E} | < \infty$ $\lim_{r \to \infty} r |\underline{E}| < \infty$ ,
  
  $lim_{r \to \infty} r | \underline{H} | < \infty$ $\lim_{r \to \infty} r |\underline{H}| < \infty$
  
  $lim_{r \to \infty} r | \underline{E} - ζ \underline{H} \times {\underline{i}}_{r} | = 0$ $\lim_{r \to \infty} r |\underline{E}-\zeta \underline{H} \times \underline{i}_r| = 0$ .
Punto campo vicino al dipolo elementare

Per $\beta r \ll 1$ si possono trascurare tutti i termini delle espressioni tra parentesi quadre nelle espressioni del campo, ed $e^{-j β r} è circa uguale a 1, perciò:

$E_{r} = j \frac{ζ I Δ z}{2 λ r} {[\frac{1}{j β r}]}^{2} 2 \cos (ϑ)$ $E_r = j \dfrac{\zeta I \Delta z}{2 \lambda r} \left[ \dfrac{1}{j \beta r} \right]^2 2 \cos(\vartheta)$

$E_{ϑ} = j \frac{ζ I Δ z}{2 λ r} {[\frac{1}{j β r}]}^{2} \sin (ϑ)$ $E_{\vartheta} = j \dfrac{\zeta I \Delta z}{2 \lambda r} \left[ \dfrac{1}{j \beta r} \right]^2 \sin(\vartheta)$

$H_{φ} = j \frac{I Δ z}{2 \lamba r} [\frac{1}{j β r}] \sin (ϑ)$ $H_{\varphi} = j \dfrac{I \Delta z}{2 \lamba r} \left[\dfrac{1}{j \beta r} \right] \sin(\vartheta)$ .

Il campo magnetico è un infinito di ordine inferiore rispetto al campo elettrico: il campo vicino di un dipolo è essenzialmente elettrico.

1.6.2 Resistenza d'irradiazione e resistenza d'ingresso

R_{irr} = \frac{2 π}{3} ζ {(\frac{h_{M}}{λ})}^{2} ≅ 800 {(\frac{h_{M}}{λ})}^{2}

$R_{\text{irr}} = \dfrac{2\pi}{3} \zeta \left( \dfrac{h_M}{\lambda} \right)^2 \cong 800 \left( \dfrac{h_M}{\lambda} \right)^2$ .

Per ottenere la resistenza d'ingresso, si divide la resistenza di irradiazione per l'efficienza $\eta$ . Esse coincidono se non si hanno perdite (di potenza).

1.7 Dipolo corto PSW

Se il dipolo elementare ha lunghezza molto minore della lunghezza d'onda, allora si dice dipolo corto. È il più semplice caso d'antenna.

1.8 Monopolo PSW

Un'antenna monopolare consiste in un braccio di un dipolo posto sopra il terreno (o, idealmente, su un piano metallico), che funge da secondo braccio. Il monopolo deve essere appoggiato con asse perpendicolare al piano. L'altezza del monopolo dovrebbe idealmente essere $\lambda/4$ (un quarto della lunghezza d'onda della frequenza centrale). Un monopolo lungo un quarto di lunghezza d’onda posto su un piano metallico risuona e irradia, nella regione superiore al piano, lo stesso campo di un dipolo a $\lambda/2$ .

1.9 Costante di propagazione k PSW

La costante di propagazione è una costante che vale $k = \omega^2\epsilon\mu$ , e che rappresenta l'ampiezza di un vettore detto vettore di propagazione $\underline{k}$ , ortogonale ai campi elettrico e magnetico. Se la direzione $\underline{i_k}$ del vettore $\underline{k}$ è reale, l'onda è piana od omogenea. Se il vettore $\underline{k}$ è immaginario puro, l'onda è piana in cut-off (il campo si attenua senza dissipare potenza). Se $\underline{k}$ ha sia parte reale che parte immaginaria, la direzione non è reale e l'onda piana è inomogenea Se $k$ è reale, non si hanno perdite di potenza; se $k$ è complesso, si avranno delle perdite.

1.10 Onda sferica PSW

Il campo lontano di un dipolo corto o elementare è caratterizzato dal fatto che la fase è costante sulle sfere centrate sulla posizione del dipolo. Queste superfici sono dette equifase o fronti d'onda dell'onda che si propaga. Un'onda in cui le superfici equifase ed equiampiezza sono sfere concentriche è detta onda sferica. L'insieme di superfici equifase individua un insieme di curve, dette raggi, che sono in ogni punto ortogonali a una superficie equifase. Se approssimiamo la superficie sferica col suo piano tangente, si ha un'onda piana, in cui i raggi sono tra loro paralleli. In una zona limitata è possibile effettuare tale approssimazione, con un errore di fase, che si considera accettabile se al di sotto di 5°.

1.11 Antenna PSW

L'antenna è una struttura, generalmente fatta in un buon materiale conduttore, avente dimensione e forma tali da irradiare la radiazione elettromagnetica nel modo più efficiente possibile. L'onda elettromagnetica è generata da un conduttore che alimenta l'antenna con una corrente variabile nel tempo. Siccome correnti che variano nel tempo irradiano onde elettromagnetiche, si eccitano le correnti variabili nel tempo sull'antenna collegandola a una sorgente opportuna, di solito per mezzo di una linea di trasmissione o di una guida d'onda. Per irradiare in modo efficiente, la dimensione minima dell'antenna deve essere paragonabile alla lunghezza d'onda. Se la densità di corrente J eccitata sull'antenna è nota, si può calcolare il campo elettromagnetico irradiato. Il problema è determinare la corrente J tale che il campo risultante soddisfi le condizioni al contorno dell'antenna. Il modo di evolversi delle onde elettromagnetiche nel tempo e nello spazio è descritto dalle leggi di Maxwell.

1.11.1 Antenna a lambda/2 PSW

Resistenza d'irradiazione e resistenza d'ingresso

$R_{irr} = 73.1 Ω$ $R_{\text{irr}} = 73.1\ \Omega$ .

Per ottenere la resistenza d'ingresso, si divide la resistenza di irradiazione per l'efficienza $\eta$ . Esse coincidono se non si hanno perdite (di potenza).

1.11.2 Massimo guadagno di un'antenna PSW

Il massimo guadagno possibile di un'antenna si ottiene quando essa è illuminata al massimo, e vale:

G_{MAX} = \frac{4 π}{λ^{2}} A_{eff} \leq \frac{4 π r R^{2}}{λ^{2}}

$G_{\text{MAX}} = \dfrac{4\pi}{\lambda^2}A_{\text{eff}} \leq \dfrac{4\pi r R^2}{\lambda^2}$ .

1.11.3 Antenna filiforme PSW domande

Un'antenna filiforme è composta da due aste metalliche sottili separate da un gap cui è collegata l'alimentazione, che fornisce un campo alla struttura. È caratterizzata da un parametro detto fattore di snellezza $\Omega$ :

Ω = l o g {(\frac{2 ℓ}{a})}^{2} > 10

$\Omega = log \left( \dfrac{2\ell}{a} \right)^2 > 10$

con: - $\ell$ semi-lunghezza dell'antenna;

$a \ll 2\ell$ raggio della sezione orizzontale dell'antenna.

Se l'antenna è snella, e il conduttore è un CEP, la corrente è solamente superficiale, la corrente non dipende alla componente $\phi$ ed è diretta lungo l'asse dell'antenna (che fissiamo coincidente con l'asse z). Sulle basi dell'antenna, inoltre, la corrente tende a convergere radialmente (fig. radiale)

È l'antenna più semplice possibile. () Per avere una buona efficienza, l'antenna filiforme deve avere lunghezza pari a $\lambda/2$ , con $\lambda$ lunghezza d'onda del mezzo in cui si trova l'antenna (nel caso dello spazio, il vuoto). Per descrivere matematicamente la corrente su un'antenna, si nota innanzitutto che per antenne piccole rispetto alla lunghezza d'onda $\lambda$ si ha un andamento triangolare della corrente. Per un'antenna a $\lambda/2$ si ha un andamento smussato rispetto a quello triangolare. All'aumentare di $\lambda$ , la corrente assume una forma sinusoidale.

Il campo di un'antenna è facilmente calcolabile quando è nota la distribuzione di corrente $J$ . Ben più difficile è il problema inverso: dato un campo che rispetta certe condizioni al contorno, calcolare la distribuzione di corrente $J$ che lo ha generato. Tale corrente dipende infatti dalla struttura e geometria della antenna nonché dal tipo di alimentazione. Di solito non si riesce a trovare la soluzione esatta del problema, ma quella approssimata con un certo grado di errore che si fa in modo di rendere il più piccolo possibile.

Un'antenna può essere alimentata usando una linea di trasmissione o un'alimentazione coassiale attraverso il piano di terra. Questi sistemi di alimentazione influenzano direttamente le caratteristiche di impedenza dell'antenna

Modello di alimentazione a delta-gap

L'alimentazione a delta-gap modella la sorgente assumendo che il campo elettrico esista solo nel piccolo gap tra i due terminali dell'antenna. Il campo sul gap è uniforme e assiale (cioé diretto lungo z, cioè l'asse dell'antenna). Il campo tangente sul cilindro di conduttore è nullo: $\underscore{i}_n \times \underscore{E} = \underscore{0}$ . Sulle basi dell'antenna la corrente tende a convergere radialmente e tende a zero al centro delle basi del cilindro.
Equazione di Pocklington PSW

L'equazione di Pocklington è uno strumento utile per ottenere la distribuzione di corrente sull'antenne. Precisamente, è un'equazione al cui interno compare la densità di corrente dentro un'integrale. Tale densità di corrente può poi essere ricavata ad esempio con metodi numerici.

La densità di corrente sulla superficie di un'antenna è data dall'equazione:

$\underline{J} = I (z) \frac{1}{2 π a} δ (r - a) \underscore i_{z}$ $\underline{J} = I(z) \dfrac{1}{2\pi a} \delta (r - a) \underscore{i}_z$

con $a$ raggio della sezione del filo. L'incognita è la corrente totale $I(z)$ che fluisce attraverso una certa sezione dell'antenna:

$I (z) = \int \underline{J} \cdot {\underline{i}}_{z} d S$ $I(z) = \int{\underline{J} \cdot \underline{i}_z dS}$ .

Per trovare la densitià di corrente $\underline{J}$ si considera il potenziale vettore associato al campo $\underline{E}_S$ prodotto dalla corrente $\underline{J}$ :

$\underline{A} = A_z \underline{i}_z = A_z(\underscore{r},\underscore{r'}) = \dfrac{\mu_0}{4\pi} \int_{\text{superficie antenna}}{ \dfrac{I(z')}{2\pi a} \dfrac{e^{-jk|\underline{r}-\underline{r}'|}} {{|\underline{r}-\underline{r}'|}} a d\phi dz'$ $\underline{A} = A_z \underline{i}_z = A_z(\underscore{r},\underscore{r'}) = \dfrac{\mu_0}{4\pi} \int_{\text{superficie antenna}}{ \dfrac{I(z')}{2\pi a} \dfrac{e^{-jk|\underline{r}-\underline{r}'|}} {{|\underline{r}-\underline{r}'|}} a d\phi dz'$ ,

con $\underline{r}$ vettore punto campo ed $\underline{r}'$ vettore punto sorgente, entrambi posti lungo l'asse dell'antenna. Dev'essere:

${\underline{i}}_{n} \times {\underline{E}}_{S} = {\begin{cases} \underline{0} & fuori dal gap \\ - {\underline{i}}_{n} \times {\underline{E}}_{g} & sul gap \end{cases}$ $\underline{i}_n \times \underline{E}_S = \begin{cases} \underline{0} &\text{fuori dal gap}\\ -\underline{i}_n \times \underline{E}_g &\text{sul gap} \end{cases}$ ,

ovvero: il campo elettrico lungo z tangente all’antenna deve essere nullo fuori dal gap e pari a $-\underline{E}_g$ sul gap.

Va semplificata l'espressione del potenziale vettore, tenendo conto delle caratteristiche del problema.

Si considera la parte di integrale in $d\phi$ , che rappresenta il campo di una distribuzione di corrente posta su un anello dell'antenna. Per la geometria del problema, la distanza $\underline{r}-\underline{r}'$ è indipendente da $\phi$ , così come lo è il ritardo di fase. Perciò si ha:

$\int_{superficie anello} \frac{e^{- j k | \underline{r} - {\underline{r}}^{'} |}}{| \underline{r} - {\underline{r}}^{'} |} d ϕ = \int_{0}^{2 π} \frac{e^{- j k | \underline{r} - {\underline{r}}^{'} |}}{| \underline{r} - {\underline{r}}^{'} |} d ϕ ≅ \frac{e^{- j k | \underline{r} - z^{'} {\underline{i}}_{z} |}}{| \underline{r} - z^{'} {\underline{i}}_{z} |} 2 π$ $\int_{\text{superficie anello}}{\dfrac{e^{-jk|\underline{r}-\underline{r}'|}}{|\underline{r}-\underline{r}'|}d\phi} = \int_{0}^{2\pi}{{\dfrac{e^{-jk|\underline{r}-\underline{r}'|}}{|\underline{r}-\underline{r}'|}d\phi}} \cong \dfrac{e^{-jk|\underline{r}-z' \underline{i}_z|}}{|\underline{r}-z' \underline{i}_z|} 2\pi$

ponendo $\underline{r}' \simeq z'\underline{i}_z$ essendo snella l'antenna. Si ottiene quindi:

$$$ $$$ $A_{z} ≃ \frac{μ_{0}}{4 π} \int_{superficie antenna} \frac{I (z^{'})}{2 π a} \frac{e^{- j k | \underline{r} - z^{'} {\underline{i}}_{z} |}}{| \underline{r} - z^{'} {\underline{i}}_{z} |} a 2 π d z^{'} = \frac{μ_{0}}{4 π} \int_{-l}^{+l} I (z^{'}) \frac{e^{- j k | \underline{r} - z^{'} {\underline{i}}_{z} |}}{| \underline{r} - z^{'} {\underline{i}}_{z} |} d z^{'}$ $A_z \simeq \dfrac{\mu_0}{4\pi}\int_{\text{superficie antenna}} \dfrac{I(z')}{2\pi a} \dfrac{e^{-jk|\underline{r}-z' \underline{i}_z|}}{|\underline{r}-z' \underline{i}_z|} a 2\pi dz' = \dfrac{\mu_0}{4\pi} \int_{\text{-l}}^{\text{+l}} I(z') \dfrac{e^{-jk|\underline{r}-z' \underline{i}_z|}}{|\underline{r}-z' \underline{i}_z|} dz'$ .

Il campo elettrico è legato al potenziale vettore dall'equazione:

$\underline{E} = - j ω \underline{A} - \frac{j ω}{k_{0}^{2}} \underline{\nabla} (\underline{\nabla} \cdot \underline{A})$ $\underline{E} = -j\omega \underline{A} - \dfrac{j\omega}{k_0^2}\ \underline{\nabla}(\underline{\nabla}\cdot \underline{A})$

con $\omega$ frequenza angolare, $k_0$ costante di propagazione (MazzarellaCampi1kpropagaz) e

$\underline{\nabla} (\underline{\nabla} \cdot \underline{A}) = \underline{\nabla} (\frac{δ A_{z}}{δ z}) = \frac{δ^{2} A_{z}}{δ z^{2}} {\underline{i}}_{z}$ $\underline{\nabla}(\underline{\nabla}\cdot \underline{A}) = \underline{\nabla}\left( \dfrac{\delta A_z}{\delta z} \right) = \dfrac{\delta^2 A_z}{\delta z^2}\ \underline{i}_z$ termine che coincide col gradiente del potenziale scalare $\Phi$ . Perciò:

$\underline{E} = - j ω \underline{A} - \frac{j ω}{k_{0}^{2}} \frac{δ^{2} A_{z}}{δ z^{2}} {\underline{i}}_{z} = - j ω (1 + \frac{1}{k_{0}^{2}} \frac{δ^{2}}{δ z^{2}}) A_{z} {\underline{i}}_{z}$ $\underline{E} = -j\omega \underline{A} - \dfrac{j\omega}{k_0^2} \dfrac{\delta^2 A_z}{\delta z^2} \underline{i}_z = -j\omega \left( 1 + \dfrac{1}{k_0^2} \dfrac{\delta^2}{\delta z^2} \right) A_z \underline{i}_z$ .

Sostituendo nell'ultima equazione l'espressione di $A_z$ precedentemente trovata, si ottiene l'equazione di Pocklington:

$- j ω (1 + \frac{1}{k_{0}^{2}} \frac{δ^{2}}{δ z^{2}}) \frac{μ_{0}}{4 π} \int_{- ℓ}^{+ ℓ} I (z^{'}) \frac{e^{- k j R}}{R} d z^{'} = {\begin{cases} 0 & fuori dal gap \\ - E_{g} & sul gap \end{cases}$ $-j\omega \left( 1 + \dfrac{1}{k_0^2} \dfrac{\delta^2}{\delta z^2} \right) \dfrac{\mu_0}{4\pi} \int_{-\ell}^{+\ell} I(z') \dfrac{e^{-kjR}}{R} dz' = \begin{cases} 0 &\text{fuori dal gap}\\ -E_g &\text{sul gap} \end{cases}$ .

L'equazione ha un problema di singolarità, ed è presente una discontinuità che causa un errore. È inoltre necessario far sì che sia sempre $\underline{r} \neq \underline{r}'$ .
Equazione di Hallén PSW

$\underline{E} = - j ω (A_{z} + \frac{1}{k_{0}^{2}} \frac{δ^{2} A_{z}}{δ z^{2}}) = {\begin{cases} 0 & fuori dal gap \\ - E_{g} & sul gap \end{cases}$ $\underline{E} = -j\omega \left( A_z + \dfrac{1}{k_0^2} \dfrac{\delta^2 A_z}{\delta z^2} \right) = \begin{cases} 0 &\text{fuori dal gap}\\ -E_g &\text{sul gap} \end{cases}$ ,

$$$ $$$
Antenne corte
Antenne a doppia banda

Si può realizzare un'antenna a doppia banda di frequenza inserendo un circuito parallelo condensatore/induttanza su ciascun braccio dell'antenna. Si vuole ottenere un'antenna che a una certa frequenza $f_H$ funzioni come un'antenna a mezz'onda, e a una frequenza $f_L$ come un'antenna corta.

1.11.4 Antenne stampate PSW

Se la frequenza è elevata, generalmente non si utilizzano antenne filiformi, bensì antenne stampate.

1.11.5 Antenna monomodale PSW

Antenna per cui la forma della corrente non dipende dalla presenza delle altre antenne, ma ne dipende solo l'ampiezza.

1.11.6 Antenne in ricezione PSW

Si consideri un'antenna immersa in un campo elettromagnetico incidente $(\underline{E}_i, \underline{H}_i)$ viene collegata a un utilizzatore (es. una linea di trasmissione). L'antenna può essere vista mediante il suo circuito equivalente, la cui resistenza d'ingresso è quella vista a vuoto ai morsetti dell'antenna, e la tensione a vuoto $V_0$ è ricavata tramite il prodotto scalare tra il campo incidente che arriva sull'antenna, calcolato come se l'antenna non ci fosse, e l'altezza efficace in ricezione (che determina i parametri dell'antenna in ricezione): $V_0 = \underline{h}_{\text{ricezione}} \cdot \underline{E}_i = \underline{h} \cdot \underline{E}_i$ . Per mezzi reciproci (quelli di maggiore interesse), l'altezza efficace è quella in trasmissione. Se si vuole massimizzare il campo ricevuto dall'antenna ricevente, bisogna fare in modo che tale campo sia allineato con l'altezza efficace dell'antenna ricavata in trasmissione.

La potenza che un'antenna riceve quando è investita da un'onda piana, avendo un campo incidente proveniente da una direzione $\underline{k}$ , va valutata tenendo conto del circuito equivalente dell'antenna, avente un'impedenza d'ingresso $Z_i$ e un generatore di tensione $V_0$ . L'antenna è collegata a un carico $Z_c$ . Si vuole ricavare quando il carico assorbe la massima potenza. La potenza sul carico $P_C$ è:

P_{C} = \frac{1}{2} R_{c} \frac{| V_{0} |^{2}}{| Z_{i} + Z_{c} |^{2}} = \frac{1}{2} R_{c} \frac{| \underline{h} \cdot {\underline{E}}_{i} |^{2}}{(R_{i} + R_{c})^{2} + (X_{i} + X_{c})^{2}}

$P_C = \dfrac{ 1 }{ 2 }R_c \dfrac{ |V_0|^2 }{ |Z_i + Z_c|^2 } = \dfrac{ 1 }{ 2 } R_c \dfrac{ |\underline{h} \cdot \underline{E}_i|^2 }{ (R_i + R_c)^2 + (X_i + X_c)^2 }$ .

Se il campo incidente $E_i$ è fisso, possiamo variare la potenza variando l'altezza efficace $\underline{h}$ oppure modificando l'impedenza d'ingresso $Z_in$ dell'antenna.

La potenza è massima quando $Z_c = Z_i^*$ . In tal caso si parla di adattamento del carico tra l'antenna e il carico. In tal caso si annullano i termini $X_i$ e $X_c$ .

Se vogliamo valutare quando il numeratore di $P_c$ è massimo, le due grandezze $\underline{h}$ ed $E_i$ devono essere legate tra loro dalla relazione $\underline{E}_i = \alpha \underline{h}^*$ , con $\alpha$ generico scalare complesso. La potenza massima è allora:

P_{C, max} = \frac{1}{2} R_{c} \frac{| \underline{h} |^{2} | {\underline{E}}_{i} |^{2}}{4 R_{c}^{2}} = \frac{| \underline{h} |^{2} | {\underline{E}}_{i} |^{2}}{8 R_{c}}

$P_{C, \text{max}} = \dfrac{ 1 }{ 2 } R_c \dfrac{ |\underline{h}|^2 |\underline{E}_i|^2 }{ 4R_c^2 } = \dfrac{ |\underline{h}|^2 |\underline{E}_i|^2 }{ 8R_c }$ .

È richiesto preliminarmente che antenna e campo incidente abbiano la stessa polarizzazione: solo in tal caso si ha $\underline{E}_i = \alpha \underline{h}^*$ ruotando la ricevente.

1.12 Array di antenne PSW

1.13 Lunghezza dell'antenna PSW

Un dipolo correttamente dimensionato consiste di due bracci ciascuno di un quarto di lunghezza d'onda. Nel vuoto, se la lunghezza d'onda del segnale è di un metro, ogni braccio misura un quarto di metro di lunghezza fisica.

Supponiamo che l'energia che il dipolo sta ricevendo sia sotto forma di un'onda sinusoidale. Una sinusoide completa consiste in una metà positiva e una metà negativa. Ogni braccio del dipolo è un quarto di lunghezza d'onda, quindi ogni braccio raccoglie la metà di un mezzo ciclo. Entrambi i bracci insieme, quindi, raccolgono l'intero mezzo ciclo. Questo significa che il segnale attraverso il dipolo si muove tutto nella stessa direzione, perché il mezzo ciclo di un'onda sinusoidale è positivo o negativo.

Se allunghiamo i bracci del dipolo in modo che siano di mezza lunghezza d'onda ciascuno (invece di un quarto), un braccio raccoglie il semiciclo positivo del segnale e l'altro la metà negativa del segnale. Nel punto di giunzione dei bracci, dove il ricevitore prende il segnale dal dipolo, non c'è più alcun segnale perché le due correnti opposte si annullano. Questo perché le correnti su ciascun braccio scorrono ora in direzioni diverse, dato che un braccio vede la metà di una sinusoide positiva e l'altro la metà negativa. Naturalmente, la cancellazione non è perfetta, ma è sufficiente per causare problemi.

Se i bracci sono più corti di mezza lunghezza d'onda, anche questo non è ideale. Il risultato è una minore potenza del segnale. Non stiamo più raccogliendo la maggior parte possibile di un mezzo ciclo di un'onda, quindi si ha perdita del segnale complessivo.

L'ultimo esperimento che possiamo provare è quello di aumentare notevolmente la lunghezza dei bracci del dipolo. Se li facciamo abbastanza lunghi, non c'è più la cancellazione completa nel punto di segnale alla giunzione dei bracci. Tuttavia, ci sono ancora pezzi di segnali di direzione opposta indotti sui singoli bracci, che si annulleranno ancora sui bracci stessi.

Quindi, la lunghezza ideale del braccio per un dipolo è lambda/4 (e quindi la lunghezza complessiva del dipolo dev'essere lambda/2… O multipli interi). Se è più piccola, non massimizzeremo la captazione del nostro segnale. Se la dimensione del braccio è più lunga, cominceremo a vedere effetti di cancellazione nel dipolo.

1.13.1 Dipolo a lambda/2

1.13.2 Dipolo elementare

Direttività del dipolo elementare

1.14 Polarizzazione PSW

Se un materiale reagisce a un campo elettromagnetico polarizzandosi (cioé aumentando la sua carica), allora esso risente del campo. Il campo, espresso per mezzo dei fasori delle sue componenti, descrive sol suo estremo, al variare del tempo, una curva chiusa su un piano detto piano di polarizzazione. Tale curva è un ellisse. I due casi di polarizzazione utilizzati nei sistemi di telecomunicazioni sono:

polarizzazione lineare l'ellisse degenera in un segmento di retta. Ne esistono infinite di polarizzazioni lineari, una per ciascuna direzione della retta;
polarizzazione circolare l'ellisse degenera in una circonferenza. Esistono due polarizzazioni circolari, una per ciascun verso con cui si percorre la circonferenza.

Ogni sistema di comunicazione ha una sua polarizzazione, e le antenne devono avere la stessa polarizzazione: in caso contrario si ha perdita di potenza. Nella telefonia si utilizza la polarizzazione circolare, per avere un collegamento indipendente dell'orientazione dell'antenna ricevente: rispetto alla polarizzazione lineare si ha un'efficienza del 50%, qualunque sia la posizione del terminale mobile (ma si perdono 3 dB di potenza). Sia:

\underline{E} = E_{x} \underline{i_{x}} + E_{y} \underline{i_{y}} = \underline{A} + j \underline{B}

$\underline{E} = E_x\underline{i_x} + E_y\underline{i_y} = \underline{A} + j\underline{B}$

\underline{A} = (A_{x}, A_{y}), \underline{B} = (B_{x}, B_{y})

$\underline{A} = (A_x, A_y), \underline{B} = (B_x, B_y)$

Le condizioni per avere polarizzazione circolare sono le seguenti:

$E_x = 0$ ;
$E_y = 0$ ;
$\phase{E_x} = \phase{E_y} + \pi + n\pi$ ;

si deve verificare almeno una delle tre condizioni precedenti. La condizione può anche essere espressa mediante l'identità $\underline{A} \times \underline{B} = \underline{0}$ .

Le condizioni per avere polarizzazione lineare sono le seguenti (devono essere soddisfatte entrambe):

$|E_x|=|E_y|$ ;
$\phase{E_x} = \phase{E_y} + \dfrac{\pi}{2} + n\pi$

o, in termini di componenti $\underline{A}$ e $\underline{B}$ (le condizioni devono essere soddisfatte entrambe):

$\underline{A} ⋅ $\underline{B} = 0$ ;
$|\underline{A}| = |\underline{B}|$ .

1.14.1 Polarizzazione nella telefonia cellulare

Per i terminali cellulari si utilizza la polarizzazione circolare per avere un collegamento indipendente dall'orientazione dell'antenna ricevente. Spesso però si utilizzano antenne polarizzate linearmente, accettando una perdita di 3 dB nel collegamento (cioé spreco sempre metà della potenza di trasmissione, ma l'efficienza è costante ).

1.14.2 Rapporto assiale

Il rapporto assiale è una misura della qualità della polarizzazione. È il rapporto tra il massimo del modulo del campo (espresso in funzione del tempo), e il modulo del minimo del campo. Se il rapporto assiale vale 1, la polarizzazione è circolare, se tende a infinito, la polarizzazione è lineare.

1.14.3 Componenti co-polare e cross-polare

Il campo irradiato $E_{\text{irr}}$ può essere decomposto in una componente $E_c$ nella polarizzazione nominale (componente co-polare) e una componente $E_x$ a essa ortogonale (componente cross-polare). Ci interessa la componente co-polare. L'altra componente va limitata in quanto comporta uno spreco di guadagno, un abbassamento di efficienza dovuto a disadattamento in polarizzazione.

1.15 TODO Campo lontano di una distribuzione di correnti PSW

Si consideri il campo prodotto da un'antenna.

Se la distanza tra il punto campo e un qualunque punto della sorgente è grande rispetto alla lunghezza d'onda:

β | \underline{r} - \underline{r^{'}} | ≫ 1, \forall {\underline{r}}^{'}

$\beta |\underline{r}-\underline{r'}| \gg 1, \forall \underline{r}'$ ;

se la distanza r tra il punto campo e il centro della minima sfera di diametro D contenente completamente l'antenna è tale che:

r ≫ \frac{D}{2}

$r \gg \dfrac{D}{2}$

allora è possibile introdurre delle semplificazioni nell'espressione del campo. Si dice che che il punto campo è in campo lontano, o in zona di Fraunhofer. Se siamo in zona di Fraunhofer, due diversi dipoli posti in due punti della sorgente P' e P'', aventi stessa direzione, hanno angoli tra le loro direzioni e il punto campo, $\vartheta'$ e $\vartheta''$ , che possono essere considerati uguali all'angolo formato dal dipolo posto al centro della sorgente e il punto campo.

Inoltre, se la quantità:

\frac{β (r^{'})^{2}}{2 r}

$\frac{\beta (r')^2}{2r}$

è piccola, allora i ritardi di fase tra ogni punto della sorgente e il punto campo sono calcolabili considerando i raggi paralleli.

1.16 Zone di campo PSW

Riportando le relazioni 1, 2, 3 e 4 della zona di Fraunhofer su un grafico avente in ascissa $Ds/\lambda$ ed $r/\lambda$ in ordinata, si ottiene un grafico in cui sono presenti varie zoni in cui utilizzare delle approssimazioni piuttosto che altre.

1.16.1 Zona di Fraunhofer (o di campo lontano)

È la zona raggiungibile da antenne di piccole dimensioni o da antenne più grandi ma a grande distanza. Il campo irradiato è un'onda piana e la fase varia linearmente con la distanza. Si può porre: $|r-r'| \simeq r- \underline{i}_r \cdot \underline{r}'$ . I campi variano come $e^-{j{\beta}r}$ . La zona di Fraunhofer è individuata da tre condizioni, le quali permettono di esprimere il campo irradiato nella forma:

\underline{E} = j \frac{ζ I \underline{h}}{2 λ r} e^{j β r}

$\underline{E} = j \dfrac{\zeta I \underline{h}}{2\lambda r} e^{j\beta r}$ .

Queste tre condizioni sono:

condizione sull'ampiezza $\beta r \gg 1$
condizione sull'ampiezza $r \gg D_s / 2$
condizione sulla fase $\dfrac{\beta}{2r} \left(\dfrac{D_s}{2} \right)^2 \ll 1$ .

Considerando un errore di ampiezza del 10% e di fase di $\boldmath{\pi/8}$ , le tre condizioni possono essere espresse come:

$r > \frac{D_{s}}{2} + \frac{5 λ}{π}$ $r > \dfrac{D_s}{2} + \dfrac{5\lambda}{\pi}$
$r > 5 D_{s}$ $r > 5D_s$
$r > \frac{2 D_{s}^{2}}{λ}$ $r > \dfrac{2D_s^2}{\lambda}$ .

Si può considerare la sorgente come puntiforme se:

$D_{s} < \frac{π}{4} \frac{λ}{2 π} = \frac{λ}{8}$ $D_s < \dfrac{\pi}{4} \dfrac{\lambda}{2\pi} = \dfrac{\lambda}{8}$ .

La zona di Fraunhoufer o di campo lontano è la zona per cui valgono le condizioni auspicabili in un collegamento tra antenne. Il campo irradiato è un'onda piana e la fase varia linearmente con la distanza. I campi variano quindi come $e^{-j\beta r}$ .

Potenza in campo lontano

$G = \frac{4 π r^{2} | E_{c} |^{2} / 2 ζ}{P_{IN}} \leq \frac{4 π r^{2} | E_{irr} |^{2} / 2 ζ}{P_{IN}}$ $G = \dfrac{4\pi r^2 |E_c|^2 / 2\zeta}{P_{\text{IN}}} \leq \dfrac{4\pi r^2 |E_{\text{irr}}|^2 / 2\zeta}{P_{\text{IN}}}$

La componente di potenza irradiata nella componente cross-polare è potenza persa, e va ridotta.

1.16.2 Zona di Fresnel

In questa zona i termini di fase vanno considerati sferici. Se siamo in presenza di sorgenti molto grandi, cade la disuguaglianza sulla fase (relazione 3) delle relazioni di Fraunhofer del campo. Nell'espressione del campo irradiato si aggiunge un termine addizionale dello sviluppo in serie del fattore di fase. Il campo varia quadraticamente rispetto alla distanza con la sorgente, e l'onda non è piana.

1.16.3 Zona dei campi radiativi

La sorgente ha dimensioni troppo elevate e non può essere vista come puntiforme. La fase e la distribuzione di potenza radiale variano rapidamente e in maniera irregolare. Se le sorgenti sono di dimensioni elevate e i campi sono vicini, la sorgente non si può considerare puntiforme, bensì estesa. Sia la fase sia la potenza radiale variano in modo rapido e irregolare.

1.16.4 Zona dei campi reattivi

Si può considerare la sorgente come puntiforme, ma non essendo grande la distanza tra sorgente e ricevitore, allora va considerato il contributo dei campi reattivi. È una zona tale per cui si è in prossimità dell'antenna. Quindi si hanno sorgenti piccole e si è vicini alla sorgente. Oltre al campo irradiato, si ha un'energia immagazzinata dalla sorgente, "avvertita" dal punto campo, a causa della vicinanza della sorgente. Nell'espressione del campo irradiato vanno considerati termini in $r^2$ ed $r^3$ nello sviluppo in serie del fattore di fare.

1.17 Altezza efficace PSW

Un'antenna in trasmissione è completamente caratterizzata dalla sua altezza efficace: essa è caratteristica di ciascuna antenna e fornisce le proprietà direzionali dell'antenna stessa, ovvero come il campo varia rispetto alle direzioni angolari θ, φ. Inoltre l'altezza efficace indica anche l’orientazione del campo elettrico. Sempre dalle proprietà del campo lontano, risulta che h deve essere ortogonale a $i_r$ . Ha le dimensioni di una lunghezza.

1.18 Area efficace PSW

Se l'antenna è adattata (sia di carico che di polarizzazione) si può definire la sua area efficace $A$ , che è il rapporto tra la massima potenza che può ricevere e il vettore di Poynting dell'onda piana incidente sull'antenna:

A = \frac{P_{C, max}}{| S_{i} |} = \frac{ζ | \underline{h} |^{2}}{4 R_{c}}

$A = \dfrac{ P_{ C, \text{ max } } } { |S_i| } = \dfrac{ \zeta |\underline{ h }|^2 }{ 4R_c }$ .

Il rapporto tra l'area efficace e il guadagno è:

\frac{A}{G} = \frac{λ^{2}}{4 π}

$\dfrac{ A }{ G } = \dfrac{ \lambda^2 }{ 4\pi }$

si evince che il guadagno, a parità di dimensioni dell'antenna, cresce con la frequenza (col quadrato della frequenza). Se l'antenna è uniformemente alimentata, l'area efficace e l'area fisica dell'antenna coincidono.

1.19 Resistenza d'irradiazione e resistenza d'ingresso PSW

La resistenza d'irradiazione $R_{irr}$ è una resistenza fittizia che dissipa tanta potenza quanta ne viene irradiata dall'antenna, a parità di valore efficace della corrente. La resistenza d’ingresso $R_{IN}$ è data dalla somma della resistenza d'irradiazione e della resistenza $R_{perdita}$ di perdita in calore dovuta ai conduttori non perfetti utilizzati nella costruzione del dipolo. L'espressione dell'impedenza d'ingresso è: $Z_{IN} = R_{perdita} + R̄_{irr} + jX_{reattiva}$ , con $jX_{reattiva}$ reattanza. La reattanza può essere negativa (reattanza capacitivà) o positiva (reattanza induttiva). Si può compensare la reattanza con dispositivi di adattamento.

Per un dipolo elementare, la resistenza d'irradiazione è:

R_{i r r} = 800 {(\frac{h_{M}}{λ})}^{2}

$R_{irr} = 800\ \left( \dfrac{h_M}{\lambda} \right)^2$

con $h_M$ altezza efficace massima. Per un'antenna a λ/2:

R_{i r r} = 73.1 Ω

$R_{irr} = 73.1\ \Omega$ .

In assenza di perdite, la potenza irradiata $P_{irr}$ è uguale alla potenza che entra nei morsetti $P_{IN}$ , e $R_{IN}=R_{irr}$ . Allora:

P_{I N} = \frac{1}{2} R_{I N} | I_{0} |^{2} = P_{i r r} = \frac{1}{2} R_{I N} | I_{0} |^{2}

$P_{IN} = \dfrac{1}{2}R_{IN}|I_0|^2 = P_{irr} = \dfrac{1}{2}R_{IN}|I_0|^2$ .

In presenza di perdite, si ha una potenza dissipata sull'antenna $P_D$ :

P_{I N} = P_{i r r} + P_{D}

$P_{IN} = P_{irr} + P_D$ .

Introducendo l'efficienza $\eta = P_{irr} / P_{IN}$ :

R_{I N} = \frac{1}{η} R_{i r r}

$R_{IN} = \dfrac{1}{\eta}R_{irr}$ .

1.20 TODO Direttività e guadagno cercareCoeffRiflessione PSW

L'altezza efficace è una misura dell'irradiazione dell'antenna, legata al campo. La direttività $D=D(\vartheta,\varphi)$ è una misura della potenza, legata al campo. È il rapporto tra la potenza irradiata in una direzione e quella media, ovvero la capacità di concentrare la potenza in una direzione:

D = lim_{r \to - \infty} \frac{S (ϑ, φ)}{(\frac{1}{4 π r^{2}}) P_{i r r}} = lim_{r \to - \infty} \frac{\frac{1}{2 ζ} | E |^{2}}{\frac{1}{4 π} \int \frac{1}{2 ζ} | E |^{2} d Ω} = \frac{| h (ϑ, φ) |^{2}}{\frac{1}{4 π} \int | h (ϑ, φ) |^{2} d Ω}

$D = \lim_{r \to -\infty} \dfrac{S(\vartheta,\varphi)}{{ \left( \dfrac{1}{4\pi r^2} \right) \ P_{irr}}} = \lim_{r \to -\infty}\dfrac{\dfrac{1}{2\zeta}|E|^2}{\dfrac{1}{4\pi}\int \dfrac{1}{2\zeta}|E|^2 d\Omega} = \dfrac{|h(\vartheta,\varphi) |^2}{\dfrac{1}{4\pi} \int{ |h(\vartheta,\varphi) |^2 d\Omega}}$ .

Per tenere conto delle perdite, si introduce il guadagno $G$ (che è una grandezza più importante della direttività):

G = lim_{r \to - \infty} \frac{S (ϑ, φ)}{\frac{1}{4 π r^{2}} P_{I N}} = η D

$G = \lim_{r \to -\infty} \dfrac{S(\vartheta,\varphi)}{\dfrac{1}{4\pi r^2}P_{IN}} = \eta D$ .

Il guadagno dipende dall'alimentazione, ma non la direttività. Qualora l'antenna sia alimentata da una linea di trasmissione e non vi sia adattamento, allora in ingresso all'antenna si ha un coefficiente di riflessione sulla linea $\Gamma \neq 0$ . Si definisce allora il guadagno realizzato $G_R$ : l'antenna va collegata a una sorgente che la deve alimentare (es. linea di trasmissione). Se si ha un disadattamento di impedenza, si ha un coefficiente $\Gamma$ di riflessione all'interfaccia diverso da zero, quindi la potenza che arriva all'antenna viene in parte trasmessa alla stessa ( $P_{\text{IN}}$ ), e in parte viene riflessa verso il generatore stesso. Questa potenza riflessa, oltre a essere persa, può danneggiare la struttura. L'espressione del guadagno realizzato è la seguente:

G_{R} = G \frac{P_{I N}}{P_{D}} = G (1 - | Γ |^{2})

$G_R = G \dfrac{P_{IN}}{P_D} = G(1 - |\Gamma|^2)$ .

Per un'antenna a $\lambda/2$ , la *direttività è $D = 1.64$ .

Per un dipolo elementare, la direttività è $D = 3/2$ .

1.21 Potenza ricevuta PSW

Si consideri il circuito seguente:

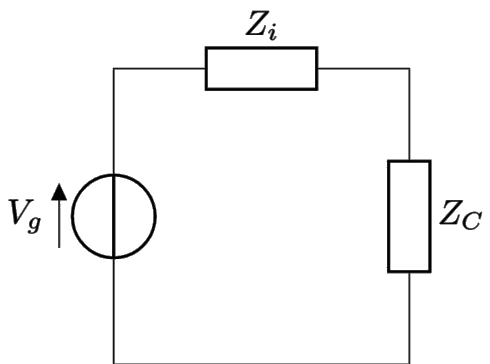
la potenza ricevuta da un carico $Z_C$ è pari a:

P_{C} = \frac{1}{2} R_{C} \frac{| V_{g} |^{2}}{| Z_{i} + Z_{C} |^{2}} = \frac{1}{2} R_{C} \frac{| \underline{h} \cdot \underline{E_{i}} |^{2}}{(R_{i} + R_{C})^{2} + (X_{i} + X_{C})^{2}}

$P_C = \dfrac{1}{2}R_C\frac{|V_g|^2}{|Z_i + Z_C|^2} = \dfrac{1}{2}R_C\dfrac{|\underline{h}\cdot\underline{E_i}|^2}{(R_i+R_C)^2+(X_i+X_C)^2}$ .

Si può massimizzare la potenza ricevuta, fissato il campo incidente, variando $Z_C$ e l'orientazione dell'antenna (e quindi $\underline{h}$ ).

Si ottiene la massima potenza rispetto a $Z_C$ con la condizione:

Z_{C} = Z_{i}^{*}

$Z_C = Z_i^*$ (condizione di adattamento del carico).

Rispetto ad $\underline{h}$ , si ha che $|V_g| \leq |\underline{h}| \cdot |\underline{E_i}|$ . La potenza massima che si può ottenere rispetto ad $\underline{h}$ (che può variare solo in direzione) è data dalla relazione $|V_g| = |\underline{h}|\ |\underline{E_i}|$ , se $\underline{E_i}=\alpha\underline{h}^*$ . L'espressione della potenza massima con adattamento in polarizzazione è:

P_{C, M A X} = \frac{1}{2} R_{C} \frac{| \underline{h} |^{2} | \underline{E_{i}} |^{2}}{4 R_{C}^{2}} = \frac{| \underline{h} |^{2} | \underline{E_{i}} |^{2}}{8 R_{C}}

$P_{C,MAX} = \dfrac{1}{2}R_C\dfrac{|\underline{h}|^2 |\underline{E_i}|^2}{4R_C^2} = \dfrac{|\underline{h}|^2|\underline{E_i}|^2}{8R_C}$ .

L'adattamento in polarizzazione richiede che antenna e campo incidente abbiano la stessa polarizzazione.

Nel caso non si abbia adattamento in polarizzazione, il fattore di depolarizzazione $DF$ ci dice di quanto si riduce la potenza ricevuta in caso di mancato adattamento. Si ha:

caso di adattamento in polarizzazione $|V_0|^2 = |\underline{h}|^2\ |\underline{E_i}|^2$ ;
caso di disadattamento in polarizzazione $|V_0|^2 = |\underline{h}|^2\ |\underline{E_i}|^2 \dfrac{|(\underline{h}^*,\underline{E_i})|^2}{|\underline{h}|^2\ |\underline{E_i}|^2} = |\underline{h}|^2\ |\underline{E_i}|^2 DF$ .

2 Sistemi radiomobili PSW

I sistemi radiomobili sono sistemi il cui collegamento radio è garantito per un certo numero di terminali su un'area detta area di servizio o area di copertura. Per garantire la copertura del servizio radio su una vasta area, quest'ultima viene suddivisa in celle, ciascuna delle quali servita da una o più stazioni radiobase (BTS, base transceiver station). Quando i canali sono esauriti (e quindi le frequenze a disposizione), si può sfruttare la divisione di spazio: le celle che sono sufficientemente lontane tra di loro riutilizzano gli stessi canali. Si parla di riuso spaziale. Si utilizzano celle più piccole laddove è presente più traffico, in caso contrario la propagazione risulterebbe difficoltosa: macrocelle, microcelle, picocelle, ecc.

Tra i sistemi radiomobili, vi sono:

sistemi broadcast utilizzano un singolo trasmettitore che trasmette in un canale di frequenza dedicato. Il trasmettitore copre un'intera area metropolitana ed è posizionato nel punto più alto disponibile, irradiando la massima potenza consentita;
sistemi di telefonia mobile l'area metropolitana è suddivisa in piccole zone, ognuna delle quali copre un'intera area metropolitana. Attraverso questa suddivisione si ovvia al problema dei limiti nella banda di frequenze. Più zone riutilizzano le stesse frequenze a disposizione: ciò è reso possibile attraverso l'attenuazione del segnale tra zone sufficientemente distanti. La lunghezza d'onda ( $\lambda=c/f$ ) è inferiore al metro, ed è di molto inferiore quindi alla dimensione degli edifici, ma maggiore della rugosità dei materiali degli edifici.

In ambiente urbano, la propagazione delle onde radio è caratterizzata da riflessione, trasmissione sulle pareti degli edifici e diffrazione. Se due zone trasmettono alla stessa frequenza, è necessario che risultino reciprocamente distanti per evitare interferenze. Al contempo il rapporto segnale/rumore del sistema di comunicazione dev'essere adeguato su ciascuna zona. Le onde radio, nella banda tra $0$ e $300\:GHz$ sono caratterizzate da lunghezze d'onda maggiori di $1\:mm$ .

3 Collegamenti wireless

3.1 PSW

3.1.1 Simboli LaTeX

Elle in corsivo minuscolo
```
$\ell$
```

3.1.2 Utili

Radiale e assiale

Differenza tra assiale e radiale

3.2 Attenuazione di un collegamento PSW

Nel caso di un segnale che si propaga nello spazio libero, l'attenuazione del collegamento varia col quadrato della distanza (formula di Friis). In realtà, va considerato il suolo, che è un conduttore che riflette, e fa sì che si crei un'oscillazione (fading) al ricevitore. In ambiente urbano (caso reale) ci sono ostacoli più o meno grandi e diffusi. Si ha un primo termine di attenuazione dovuto alla distanza tra i punti del collegamento. Gli ostcoli (case, palazzi, ecc.) causano shadow fading (oscillazioni lente) e ha andamento gaussiano. Abbiamo poi il fenomeno del fast fading (oscillazioni rapide), e sono modellate con una distribuzione probabilistica di Rayleigh o di Rice. Queste oscillazioni sono dovute al multipath. Per descrivere la propagazione in ambiente urbano si può dividere lo spazio in un piano verticale e in un piano orizzontale (laterale). Più l'antenna è collocata in alto, minore è l'attenuazione. Tuttavia non sempre è possibile porre le antenne a grandi altitudini.

3.3 Macrocelle e microcelle PSW

Si parla di macrocelle per antenne al di sopra degli edifici, di small cells se sono poste alla stessa altezza degli edifici, e di microcelle se sono al di sotto degli edifici.

3.4 Inquinamento elettromagnetico PSW

Oltre una certa soglia di frequenza, le variazioni elettromagnetiche sono ionizzanti (scompongono, cioè, le molecole dell'essere umano).